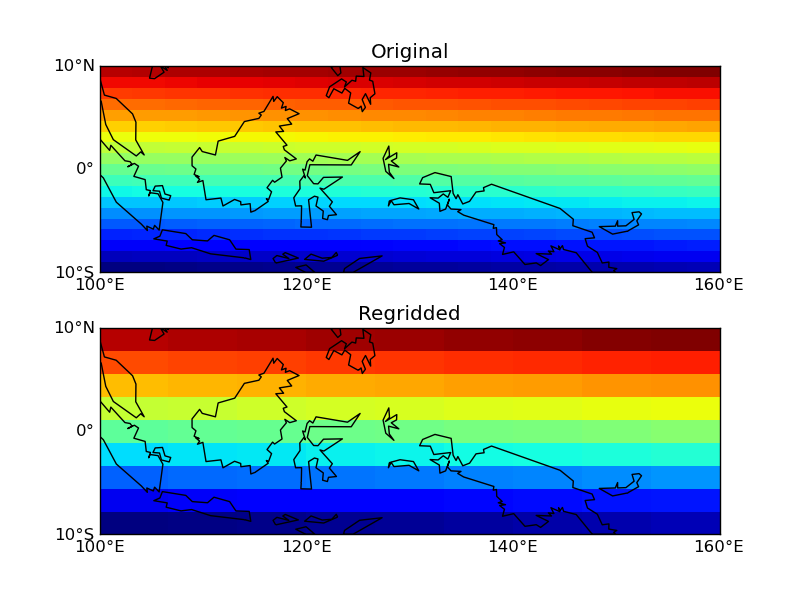
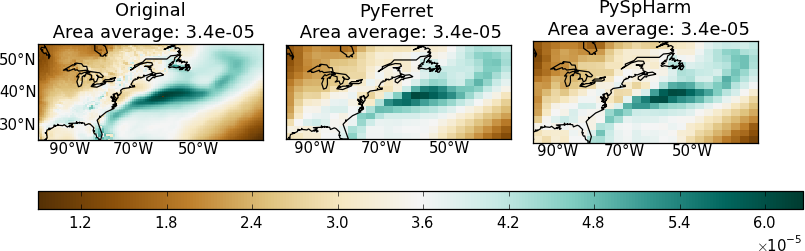
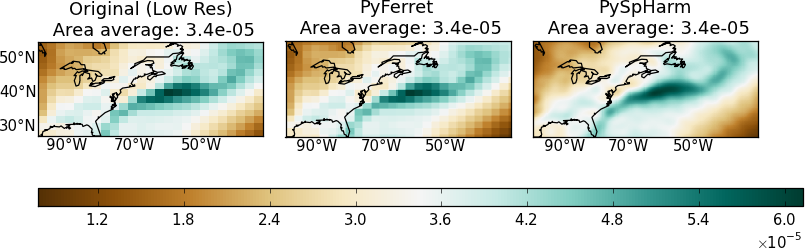
Map Regridding In Python
15 April 2014
My goal here is to regrid geographical data onto another lat-lon grid. Any library or module needed will be unloaded after the process. I have tested PyFerret and the Python spherical harmonic module (hereafter PySpHarm) and presented here how to implement PyFerret for regridding purpose. In most cases, both PyFerret and the Python and PySpHarm do a pretty good job regridding geographical 2D data and preserve area averages. Here are examples going from higher resolutions to lower resolutions and vice versa.
Pros and Cons
1. Installation - PySpHarm wins
For PyFerret, the major drawback is the fact that it is not quite trivial to install while for PySpHarm it is simple (see its documentation).
2. Annoying ripple patterns for PySpHarm - PyFerret wins
Gibbs fringes are inevitable for spectral harmonics tranforms although they can be minimised by applying filters (See Navarra 1994 and references therein). In contrast, PyFerret provides various regridding methods: linear interpolation, patch recovery by taking least squeares fit of the surrounding surface patches and conservative methods. These methods do not generate Gibbs ripples.
3. Speed - PyFerret wins
The computational complexity of the spherical harmonics transform is O(N^3) for cut-off frequency N. Some algorithms allow for a running time of O(N^2logN). I am not sure what the actual algorithm is used by PySpHarm but in my experience it is far slower than PyFerret in most cases. The performance difference is more obvious when only a region of the globe needs regridding.
Implementing PyFerret for regridding
You may download the script here. Below I present slightly more details for thoughts.
0. Preconditions
- You have installed the PyFerret module and are able to
import pyferret. If not, you may refer to my previous post on installing and building PyFerret - You should have NumPy installed as well.
1. Main action
Using PyFerret still requires some knowledge of Ferret commands. Basically my python function here is to stitch the Ferret commands together for regridding.
In Ferret, to regrid a variable SOURCE to the lat-lon grid of DEST you would write:
LET RESULT = SOURCE\[GXY=DEST\]
This is included in the function regrid_once_primitive.
What have been taken care of here:
- The data returned from Ferret may (usually) have a different axis order than the input’s. Reorder the dimensions
- Instead of specifying the axis type (T/X/Y/Z) by the users, units of the dimensions (usually available) are used for assigning the axis types. If the unit is not recognised, a normal axis is assigned
- Tranformation method can be specified
What have not been taken care of:
-
Regridding on the time axis is not implemented yet
For some reasons when pyferret is stopped, there is still memory of the previous data grid being kept so that the next time pyferret is started, dimensions of the same names used before (e.g. latitude, longitude) cannot be recognised. This might be associated with one of the known issues of PyFerret. To work around this, I use the python multiprocessing library to run the PyFerret on a separate process so that each time when the function is finished the process is killed and the memory associated is freed (I think so?).
# This decorator is a work around needed for
# calling the regrid function multiple times
def run_worker(f):
import multiprocessing
@wraps(f)
def run_func(*args,**kwargs):
P = multiprocessing.Pool(1)
result = P.apply(f,args,kwargs)
P.close()
P.terminate()
P.join()
return result
return run_func
# This is the regrid function to be called
# And it will be run as a stand-alone process that terminates after each call
regrid = run_worker(regrid_once_primitive)2. Interfaces for adding and extracting data to/from PyFerret
PyFerret.getdata and PyFerret.putdata get/read python dictionary objects. I wrote my own wrappers, __Num2Fer__ and __Fer2Num__ for converting between my input and what PyFerret asks for. For regridding purposes, you don’t need the much information needed by PyFerret, I can fill in dummy values for fields such as “title”,”dimension names”,”data_units”.
Consequently the regridding function only requests a data array, a list of coordinates, and a list of dimensions units for the input data, and the latter two for the output grid.
I also included a function __assignCAxis__ that guesses the dimension type (T/X/Y/Z) from the dimension units. This function has been very useful even in other situations. I use it a lot.
def _assignCAxis_(dimunit):
'''
Assign cartesian_axis (T/Z/Y/X) to the axis with identifiable axis units.
Axes without identifiable units will be set to None
Input: unit - a string
'''
assert type(dimunit) is str
dimunit = dimunit.split()[0]
conventions = {'T': ['second','seconds','sec','minute','minutes','min',
'hour','hours','h','day','days','d',
'month','months','mon','year','years','y'],
'Z': ['bar','millibar','decibar','atm','atmosphere','pascal','pa','hpa',
'meter','m','kilometer','km','density'],
'Y': ['degrees_north','degree_north','degree_n','degrees_n','degreen','degreesn'],
'X': ['degrees_east','degree_east','degree_e','degrees_e','degreee','degreese']}
invaxunits = { unit.lower():ax for ax,units in conventions.items() for unit in units }
return invaxunits.get(dimunit.lower(),None)3. Run
if __name__ == '__main__':
import numpy
var={}
var['data'] = numpy.arange(400.).reshape(20,20)
var['coords'] = [ numpy.linspace(-10.,10.,20),
numpy.linspace(100.,160.,20)]
var['dimunits'] = ['degrees_N','degrees_E']
ref_var={}
ref_var['coords'] = [ numpy.linspace(-10.,10.,10),
numpy.linspace(100.,160.,10)]
ref_var['dimunits'] = ['degrees_N','degrees_E']
result = regrid(var,ref_var,'XY')Results: